
Формула Тейлора. Разложение по формуле Маклорена некоторых элементарных функций
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше. Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике. Договоримся обозначать дифференциал функции переменных в точке М пространства символом Докажем следующую важную теорему. Теорема Пусть — целое число, функция задана в некоторой -окрестности точки раз дифференцируема в указанной окрестности.





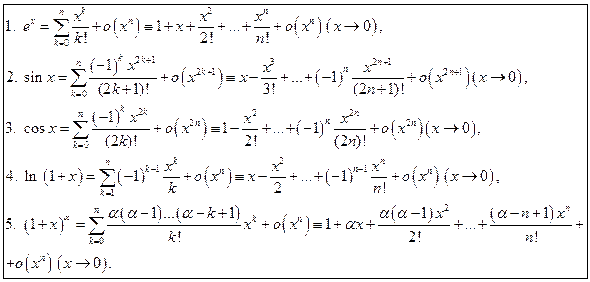


Чтобы найти первую производную в нуле, нам придётся воспользоваться определением — просто так применить стандартные правила дифференцирования не получится, так как функция по-разному опрделена в нуле и вне нуля. Дальше можно продолжать в том же духе. Каждый раз будет получаться 0. Докажите, что это действительно так! Итак, мы получаем, что все производные f в нуле равны нулю. Подведём промежуточный итог.
- Существует 3 основных представления остаточного члена:
- Частный случай разложения в ряд Тейлора в нулевой точке называется рядом Маклорена. Ряды Тейлора применяются при аппроксимации функции многочленами.
- Точнее, от вашего браузера их поступает слишком много, и сервер VK забил тревогу. Обратитесь в поддержку сервиса.
- Конев В.
- 4. Формула Тейлора с остаточным членом в форме Лагранжа для функции нескольких переменных.
- В дальнейшем нам пригодится более компактное обозначение для функций, которые являются маленькими по сравнению с какими-то другими функциями.
- Тогда справедлива формула 1 , в которой. Это утверждение верно, так как оно совпадает с доказанной ранее формулой конечных приращений Лагранжа.
- Заметим, что это формула Ньютона-Лейбница:.
- Разложение функции в ряд Тейлора в окрестности бесконечности
- Пусть функция раз дифференцируема в точке.
- П одсмотрел на других сайтах. В контрольной работе номер 12 ошибок формулирования больше, чем во всех предыдущих..
- Новые калькуляторы Построить график функции Точки разрыва функции Построение графика методом дифференциального исчисления Упростить выражение. Примеры решений Интервал сходимости ряда Оригинал и его изображение Найти предел Точки разрыва функции Диф уравнения онлайн Разложение в ряд Фурье Разложение в ряд Тейлора Найти производную.


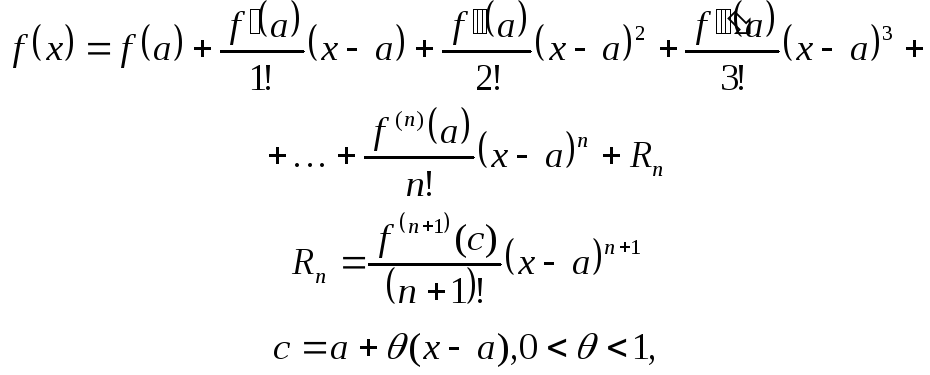











Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше. Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике. Целью этого пункта является получение формулы Тейлора для функции в окрестности произвольной точки а с остаточным членом в так называемой интегральной форме. Пусть функция имеет в некоторой -окрестности точки а непрерывную производную порядка.






